
적분반응속도식
반응물의 농도는 시간에 따라 변하기 때문에, 반응이 좀 진행된 후에는 반응속도식으로 농도를 예측하기 쉽지 않다. 때문에, 농도를 시간함수로 표현한 방정식이 필요하다. 새로운 방정식을 적분반응속도식(intrgrated rate law)이라 하며, 반응속도식에서 유도된다. 적분반응속도식이 합리적인 이유는 다음과 같다: 어떤 특정 시간에 반응계의 모든 농도를 알고, 반응속도가 시간에 따라 어떻게 변화하는지 안다면, 조금 후의 농도도 예측할 수 있다.
적분반응속도식은 반응차수에 의존한다. 몇 가지 반응차수를 갖는 일반적인 적분반응속도식을 안다면, 자료를 모델과 비교하여 반응속도식을 결정할 수 있다.
Math Connections
적분반응속도식은 반응속도식을 적분하였기 때문에 붙여진 이름이다.
우선, 가장 단순한 형태인, 한 개의 반응물에 의한 0차 반응에 대해 알아보자.
반응속도 = k[A]0 = k
속도는 시간변화에 대한 농도변화이다. △를 사용하여 식을 표현한다.
반응속도 = -△[A]/△t = k
변화를 무한소로 작게 하면, 델타를 미분으로 바꿀 수 있다.
-d[A]/dt = k
dt를 오른쪽 항으로 이동하면
d[A] = -k dt
반응의 시작인 t=0과 [A]=[A]0에서 시작하여 t와 [A]t까지 적분한다.
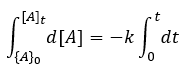
적분한 결과는 다음과 같다.
[A]t - [A]0 = -kt
이것이 0차 반응에 대한 적분반응속도식이다.
1차와 2차 반응의 적분반응속도식도 같은 방법으로 유도될 수 있다.
0차 적분반응속도식
가장 단순한 반응속도식은 0차 반응이다.
반응속도 = k[A]0 = k
0차 반응에서는, 반응물이 소비되어도 반응속도는 변하지 않는다. 적분반응속도식은
[A]t = [A]0 - kt
이 식을 재배열하여, y=mx+b의 형태로 바꾼다.
[A]t = - kt + [A]0
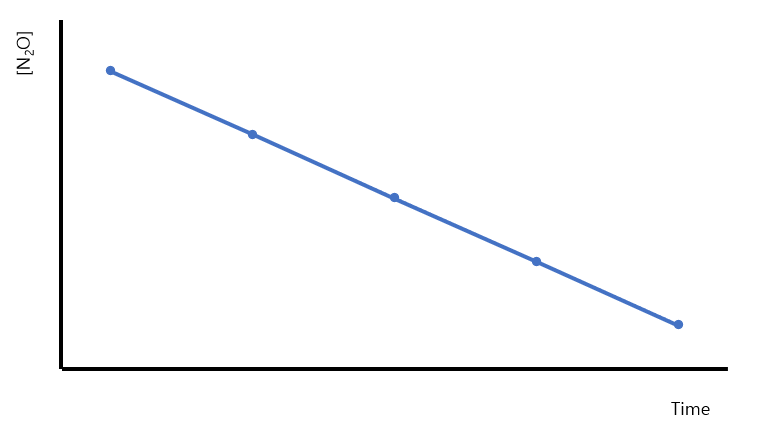
0차 반응: 시간 vs 반응물 농도에 대한 플롯은 직선이다. 기울기 = -k 반응물의 농도는 시간에 따라 직선으로 감소한다.
t (x축)에 대해 [A] (y축)를 플롯 하면 직선이 얻어진다. 직선의 기울기 m은 -k이고, y절편 b는 반응물의 초기농도인 [A]0이다. 실제 반응에서 시간함수로 반응물 A의 농도를 측정하고, [A] 대 t의 플롯을 그린다. 플롯이 직선이라면, 0차 반응일 것이다.
1차 적분반응속도식
한 개의 반응물에 대한 1차반응(d[A]/dt = -k[A])에서, 적분반응속도식은 다음과 같다.
ln[A]t/[A]0 = -kt 또는 [A]t = [A]0e-kt
[A]0는 t=0에서의 반응물의 초기농도이다. 속도상수와 초기농도를 안다면, 후속 시간에서의 농도를 예상할 수 있다.
![오존의 분해반응은 0차반응속도식을 따르지 않는다. 따라서 시간 대 [O3]를 플롯한 그래프는 직선이 아니다.](https://blog.kakaocdn.net/dna/dV89ox/btsI4sM3jKW/AAAAAAAAAAAAAAAAAAAAAN-pPdyIN-ojRFuUbhLQKL7JwWQjUIjS2AMYzCFh075M/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1772290799&allow_ip=&allow_referer=&signature=7bnrmGs0cAlWj%2BRQFUy2oyotv3M%3D)
오존의 분해반응은 0차 반응속도식을 따르지 않는다. 따라서 시간 대 [O3]를 플롯 한 그래프는 직선이 아니다.
시간 대 농도에 대해 플롯한 그래프는 직선이 아니므로, 이 반응은 0차 반응이 아니다. 다음은 1차 반응인지 확인한다. 하지만 곡선플롯은 직선만큼 판단하기 쉽지 않기 때문에, 식을 조작하여 직선식으로 만든다.
ln[A] = - kt + ln[A]0
시간 대 ln[A]의 플롯은 직선이다. ① 시간 대 [A]0의 플롯이 직선이면, 0차 반응이다. ② 시간 대 ln [A]의 플롯이 직선이면, 1차 반응이다.
2차 적분반응속도식
2차반응(d[A]/dt = -k[A]2)에서는 적분반응속도식의 수학적 형태가 1차 반응과는 매우 다르다. 반응물 A가 소비될 때, 적분반응속도식은 다음과 같다.

[A]t는 시간 t에서의 A의 농도이고, [A]0는 초기농도이다. 2차 적분반응속도식은 시간 대 1/[A]에 대해 플롯 한 그래프가 직선이며, 실험자료를 이 모델과 비교해 보고 2차 반응인지 결정한다.
반감기
반감기(half-life)는 반응물의 농도가 초기농도의 반이 되는데 걸린 시간이다. 이 값은 반응물에 한정되며, 1차 반응에서는 특히 중요하다.

1차반응에 대한 반감기를 수학적으로 표현하기 위해, t=t1/2와 [A]t=1/2[A]0을 대입하면

위는 1차 반응의 반감기로, 속도상수 k는 물질의 양에는 의존하지 않으며, 따라서 t1/2도 마찬가지이다. 반감기는 핵분열의 속도를 설명할 때 자주 사용되며, 모든 방사성붕괴과정은 1차 반응속도에 따른다.



