
압력
자동차 타이어에 공기를 주입하는 일부터 일기예보에 이르기까지, 압력이란 단어를 흔하게 접하 기 때문에 압력을 별생각 없이 받아들인다. 하지만 기체의 움직임을 과학적으로 연구하기 위해 서는 압력에 대한 전문적인 이해가 필요하다.
압력(pressure)은 단위 면적당 가해지는 힘이다.
기체의 압력을 유발하는 힘은?
대기압은 공기 분자의 무게에 의한 힘으로, 공기 분자는 중력에 의해 지표면으로 끌어당겨진다.
기압의 존재를 눈으로 볼 수는 없지만, 용기 안의 공기를 제거하면 대기압을 쉽게 설명할 수 있다. 용기 안의 공기가 더 이상 용기 벽을 지탱할 수 없을 때, 용기가 단단하더라도 대기압 때 문에 찌그러진다. 분자수가 증가할수록 분자들의 총무게도 증가하기 때문에, 대기압은 고도에 따라 달라진다.
그렇다면 용기에 갇힌 기체는 어떠한가? 풍선 안의 공기를 생각해 보자. 풍선 안의 공기는 풍선의 전체 벽면에 대해 방향은 상관없이 균일한 압력을 가한다. 분자 수준으로 확대하면, 각 기체 분자가 벽과 충돌하여 튕겨져 나오는 것을 보게 될 것이다. 각 분자가 용기 벽에 충돌하면 용기에 작은 힘들이 모여 기체압을 만든다.
압력의 측정
압력은 기체의 중요 성질 중 하나로, 압력계를 사용하여 측정될 수 있다. 표준압력계는 끝이 막힌 긴 관에 수은이 채워져 있는 것이 특징이다. (수은이 사용되는 이유는 밀도가 높으며 다른 기체와 화학적으로 반응하지 않기 때문이다.) 이때 막혀있는 관의 끝은 진공상태로 공기압력 때문에 수은이 흘러나가지 않는다.
통 안의 수은은 대기에 노출되어 있기 때문에, 공기가 위에서 누르는 압력을 받는다. 관 안의 수은기둥(수은주) 은 윗부분이 진공이라 위에서 누르는 압력은 전혀 존재하지 않는다. 관 입구는 두 곳으로부터 힘을 받는데, 통 안의 수은에 가해지는 대기압과 관 안의 수은 무게이다. 두 힘이 같을 때 관 안의 수은기둥 높이는 일정하게 유지되는데, 이 높이로 대기압이 결정된다.
압력의 단위
압력은 단위면적 당 힘으로, 힘과 면적의 SI단위가 N과 m²이기 때문에, 압력의 SI단위는 N m-2; 이다. Pa(pascal)로 불리기도 한다. 1 N은 대략 1/4 파운드의 물체에 가해지는 중력으로, 이 힘이 1 m²에 분산되면 그리 크지 않은 값이다. 즉 Pa은 상대적으로 작은 양으로, 대기압은 105 Pa 정도이다. 따라서 KPa을 사용하며, 많은 나라의 기상예보에서 사용된다.
미국의 대부분의 기상예보에서는 inch (in.Hg)로 압력을 표시하며, 학교에서는 대부분 mmHg를 사용한다. 압력계의 수은기둥의 높이는 압력에 정비례하기 때문에 mmHg 단위는 폭넓게 이용되고 있으며, torr라는 이름을 사용하기도 한다.
1 torr = 1mmHg
평균대기압의 측정과정에서 atmosphere (atm)이라는 단위가 정의되었다. 해수면에서의 평균 압력은 약 760 torr로, 1 atm은 760 torr와 같다.
1 atm = 760 torr = 101,325 Pa
기체의 법칙
모든 기체는 화학적으로 다르지만 물리적 변화에 같은 반응을 보인다. 기체의 법칙 공식을 사용하여 이런 변화의 영향을 계산할 수 있다. 기체의 물리적 성질들 간의 관계를 나타낸 이상기체방정식은 실험적 관찰에 의해 얻어진 것이다.
PV = nRT
P는 기체압력, V는 부피, n은 기체의 몰수, T는 온도, R은 기체상수(비례상수)이다. 어떤 기체든 간에 기체상수 값은 0.08206L atm mol-1 K-1 로 같다.
J. Charles는 19세기 초에 온도와 부피의 관계를 처음 조사하였다. 다른 양의 기체에 대해, 온도에 대한 부피의 값을 도표로 만들었는데, 두 도표의 선을 외삽하였더니 부피가 0일 때의 온도 가 -273.15°C로 서로 일치하였다. 이것에 근거하여 켈빈온도 눈금이 만들어졌다. 온도를 켈빈눈금으로 표현하였을 때, 부피와 온도는 정비례하는데, 이것이 샤를의 법칙이다.
기체의 법칙은 기체의 변수들 사이의 관계를 관찰한 결과를 표현하는 과정에서 나오게 되었다. R. Boyle은 기체의 압력과 부피에 대한 관계를 연구하였는데, 어떤 기체의 압력이 증가하였을 때 부피가 감소함 (또는 부피가 증가하였을 때 압력은 감소) 을 알게 되었다. 보일의 법칙에 의하면 일정 온도에서의 압력과 부피는 반비례한다. 또한 아보가드로의 법칙에 의하면 기체의 부피는 기체의 분자수에 비례한다.
이상기체방정식에서 R은 기체상수로 절대 변하지 않는 값이다. 다음에는 변수항만 모이도록 방정식을 재배열한다. 예로 압력과 부피는 변하고 몰(mol)수와 온도는 일정하다면, 방정식은 다음과 같이 재배열된다.
PV = nRT = 일정
nRT는 일정하기 때문에, PV 또한 일정하다. 즉 변화 전과 후의 P x V 가 같다는 것을 뜻 한다.
P₁V₁ = P₂V₂
이상기체법칙과 단위
이상기체법칙은 절대영도(T = 0)를 사용하는 절대온도(absolute temperature) 눈금에서만 유효하다. 이상기체법칙에서 T = 0일 경우, P 와 V 또는 둘 중 하나는 0이어야 하며, 이 상태에서는 기체가 존재하지 않는다. 하지만 T = 0°C 또는 T = 0℉일 경우에는 이 사실을 적용할 수 없다.
R = 0.08206 L atm mol-1 K-1
= 8.314 J mol-1; K-1;
= 62.37 L torr mol-1; K-1
부분압력
이상기체법칙을 이용하여 개별 기체의 성질을 결정할 수 있다. 이상기체방정식의 항목 중 어떤 것도 기체 성분과 관계되지 않는다.
이상기체방정식의 n은 공기의 전체 몰수로, 각 성분 몰수의 합이다.

기체혼합물의 관찰된 압력은 각 성분의 부분압력(partial pressure)의 합이다. 이 개념은 J. Dalton에 의해 제일 먼저 확립되었기에, 달톤의 부분압력법칙이라 불린다. 성분 기체가 이상적으로 거동하며, 다른 기체와 반응하지 않는다는 가정 하에 이 법칙이 성립한다. 임의의 기체혼합물에서, 각 성분의 부분압력을 아래와 같이 표시할 수 있다.

i는 성분 기체를 표시하는 기호이며, ni는 성분 i의 몰수이다. 혼합물의 전체압력 P는 각 성분의 부분압력의 합이며, 전체 몰수는 각 성분의 몰수의 합이다.
각 성분 기체의 농도를 몰분율(mole fraction)로 표현할 수 있다.
기체 반응에서의 화학양론
이상기체법칙은 기체의 몰수와 압력, 부피, 온도와의 관계를 제시하기 때문에, 기체가 관여된 화 학반응에서는 기체법칙을 이용하여 몰수를 계산할 수 있다. 화학양론문제를 계산하는데 몰비를 이용하듯이, 기체의 몰수로 기체의 온도, 압력, 부피를 계산할 때 기체법칙을 이용한다.
STP 조건
기체의 양을 언급할 때 기체의 온도, 부피, 압력을 함께 제시할 필요가 있다. 기체의 양을 서로 비교할 때 표준이 되는 조건을 사용하는 것이 편리하다. 기체의 표준온도와 압력(standard temperature and pressure)을 STP라 하며, 0°C 또는 273.15 K 그리고, 1 atm이다. 이상기체 방정식에 이 값을 대입하면, STP에서의 이상기체의 몰부피를 알 수 있다.
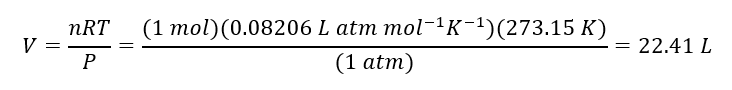
'환경화학' 카테고리의 다른 글
| 주기율표와 원자구조 2 (0) | 2024.08.05 |
|---|---|
| 주기율표와 원자구조 (0) | 2024.08.04 |
| 화학양론 (4) | 2024.07.24 |
| 분자, 몰, 화학식 2 (0) | 2024.07.19 |
| 분자, 몰, 화학식 (0) | 2024.07.18 |



